Die Entwicklung einer Schaltung
Die Entwicklung einer Schaltung folgt immer einem Muster:
- Erstellen einer Wahrheitstabelle
- Dieser Tabelle wird in KV-Tafeln aufgeteilt
- Die KV-Tafeln lassen sich nun vereinfachen
- Aus diesen KV-Tafeln lassen sich nun die Logischen Gleichungen aufstellen
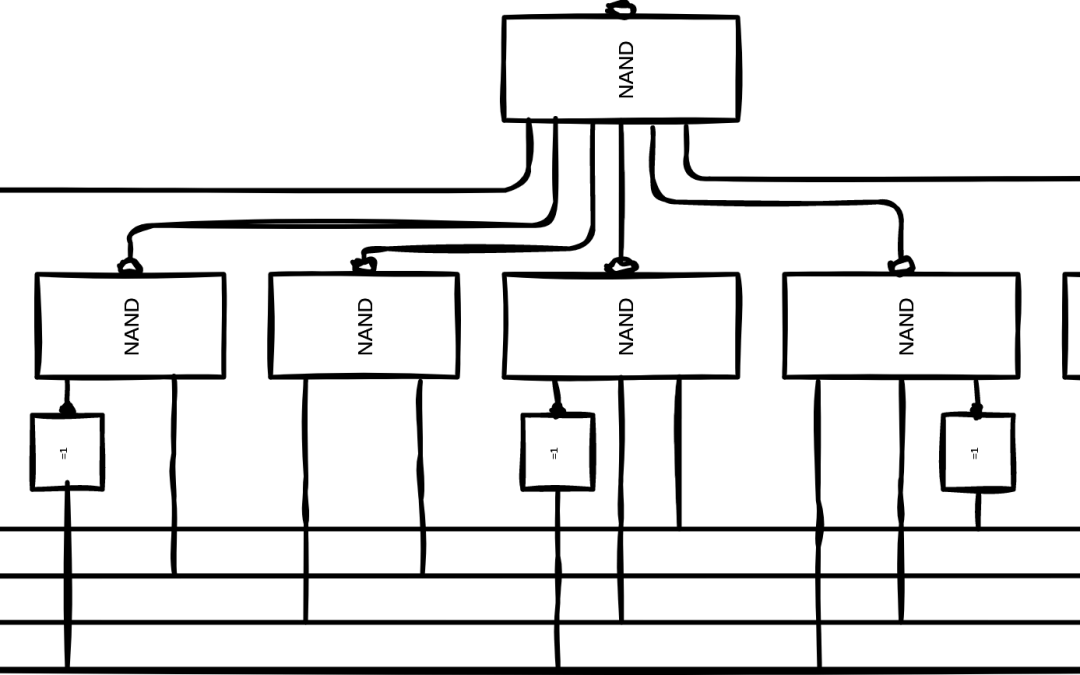
- Und zum Schluss lassen sich diese Logischen Gleichungen noch in full NAND umwandeln
Die Siebensegmentanzeige
Die Siebensegmentanzeige ist eine sehr häufig verwendete Anzeige, um Zahlen im Dezimalen, sowie auch dem Hexadezimalen Zahlensystem darzustellen. Sie wird zum Beispiel bei Fußball -oder Basketballspielen eingesetzt, um die Spielstände gut lesbar anzuzeigen. Dabei ist vor allem die einfache Struktur der Zahlen und der unkomplizierte Aufbau der Anzeige ein große Faktor für eine weite Verbreitung.
In diesem Artikel beschreibe ich den Prozess der Entwicklung einer Schaltung mit dem Beispiel der Siebensegmentanzeige.
Die Zahlen
Insgesamt lassen sich 128 mögliche Kombinationen erzeugen. Damit aber eine gute Lesbarkeit gegeben ist, wurde das Aussehen der Zahlen festgelegt.
Diese Zahlen sind die am häufigsten verwendeten Zahlen. Jedoch wird auch das Hexadezimale Zahlensystem häufig verwendet. Dazu lassen sich noch die Buchstaben A, B, C, D und F darstellen.
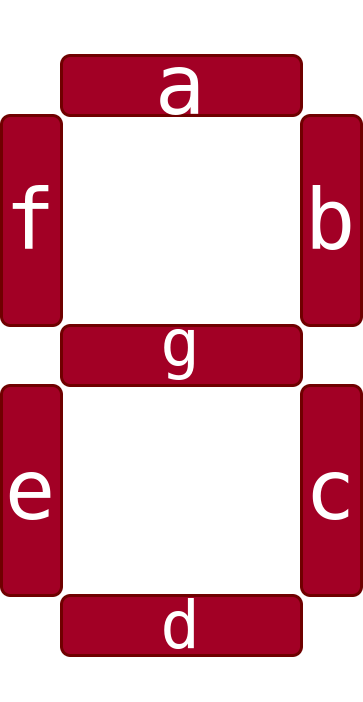
Wie bereits der Name sagt besteht die Siebensegmentanzeige aus sieben Segmenten. Diese sind wie folgt beschriftet:

![ELT-7-Segment-Anzeige-[HEX] Die Zahlen.drawio](https://blog.noweck.info/wp-content/uploads/2021/11/ELT-7-Segment-Anzeige-HEX-Die-Zahlen.drawio.png)
Die Wahrheitstabellen
Die Wahrheitstabellen sind der erster Schritt der Abstraktion. Dabei schaut man sich die Eingänge und die Ausgänge an. Bei einer Siebensegmentanzeige, welche den Hexadezimalen Zahlenraum abdecken soll, gibt es vier Eingänge und sieben Ausgänge. Die vier Eingänge kommen dadurch zustande, dass 24 die 16 Zeichen des Hexadezimalen Zahlensystems abdecken. Die Eingänge sind mit den Buchstaben W, X, Y und Z beschriftet. Die sieben Ausgänge lassen sich sehr einfach aus den sieben Segmenten der Anzeige herleiten.
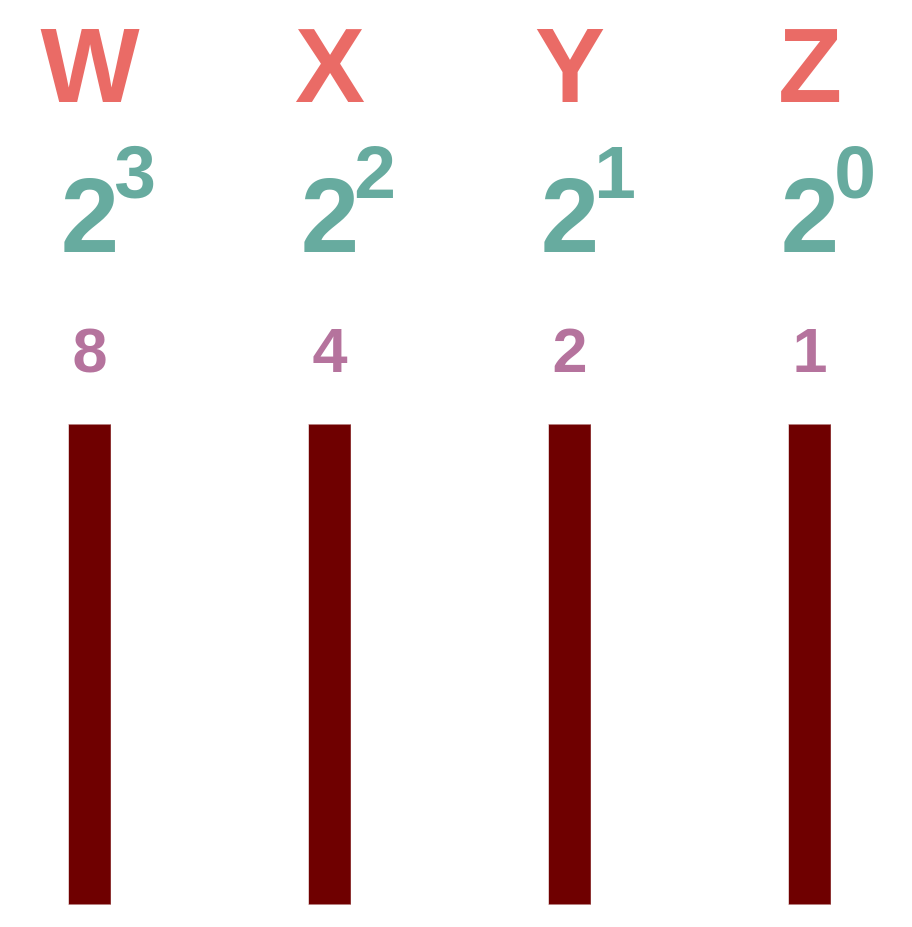

Wie die beschrifteten Segmente der Anzeige werden auch die Ausgänge beschriftet. So sollen, wenn an allen Eingänge eine Null anliegt, die Segmente a, b, c, d, e und f eingeschaltet sein. Wenn nun nur an dem Eingang Z ein Strom anliegt (also eine eins), dann sollen die Elemente b und c eingeschaltet werden. Daraus lässt sich eine Tabelle mit allen möglichen Kombinationen der Eingänge anfertigen.
Die KV-Tafeln
Jede KV-Tafel beschriebt einen Ausgabe. Also erstellen wir für jedes Segment eine eigene KV-Tafel und kommen so auf sieben Stück.
In diesen Tafeln werden die Werte aus der Wahrheitstabelle eingetragen. Dabei ist eine bestimmte Notation notwendig, um die KV-Tafel in n Dimensionen zu erweitern. In diesem Fall entspricht n unseren vier Eingängen. Um die Systematik genau zu erkennen stelle ich hier das Segment a einmal ausführlich vor. Dieses gewonnene Wissen lässt sich dann auf die anderen Segmente übertragen.

Dafür wird zunächst eine leere KV-Tafel skizziert. Jeder Eingang ist in jeder Dimension in zwei Zuständen dargestellt: Wahr (ohne Strich) für 1 & Falsch (mit Strich) für 0. Wenn an allen Eingängen eine null anliegt, so soll das Segment a eingeschaltet sein. Also suchen wir auf der KV-Tafel das Feld, auf dem alle Eingänge verneint sind. Dabei stoßen wir auf das Feld ganz oben links. Wenn nun aber eine Dezimale eins (als W=0, X=0, Y=0, Z=1) an den Eingängen anliegt, so soll das Segment ausgeschaltet sein (also eine Null beinhalten). Dieses Feld befindet sich rechts neben dem zuerst befüllten Feld. Nach diesem Verfahren befüllen wir nicht nur diese Tafel, sondern auch die für die übrigen Segmente.
KV-Tafeln vereinfachen
Um im Anschluss die logischen Gleichungen einfacher Bilden zu können, werden wir in diesem Schritt schauen, ob sich nicht einige Felder der KV-Tafel zusammen fassen lassen. Dazu versuchen wir so viele Einser wie möglich in einem Paket zusammen zu fassen. Es gibt allerdings einige Regeln zu beachten: Einser können nur waagerecht oder senkrecht zusammengefasst werden, nicht diagonal. Auch können mehrere Spalten, sowie auch Zeilen zusammen gefasst werden. Schleifen können aber auch über die KV-Tafel hinaus ragen und Felder genau gegenüber umfassen. Es ist dabei sinnvoll besonders große Schleifen zu ziehen, da dann im nächste Schritt die logischen Gleichungen nicht so lang werden.
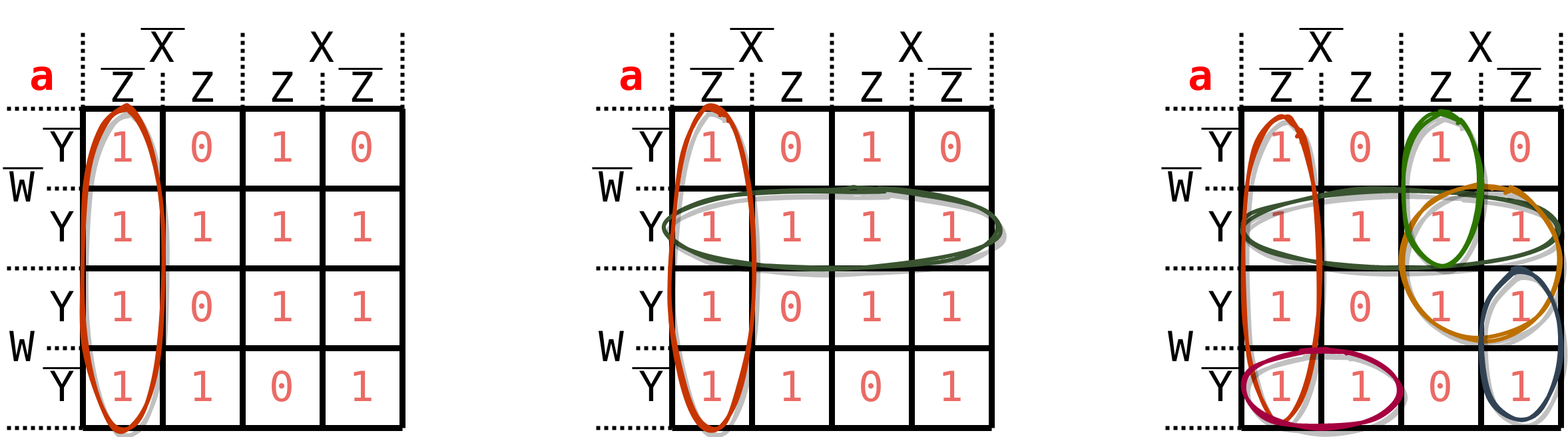
Hinweis: Hier kann sogar an einer Stelle noch ein größere Schleife gezogen werden. Überlege mal wo genau. Dadurch lässt sich im folgenden Abschnitt der logischen Gleichungen ein Eingang in einer Klammer weglassen.
Anmerkung: Eine Variation in der Anordnung der Schleifen kann im weiteren Verfahren zu unterschiedlichen logischen Gleichungen führen und dadurch auch letztendlich zu einem anderen Schaltbild. Jedoch ändert dies nicht an der Funktionalität der letztendlich entstehenden Schaltung (solang alle Schritte korrekt durchlaufen wurden).
Logische Gleichungen
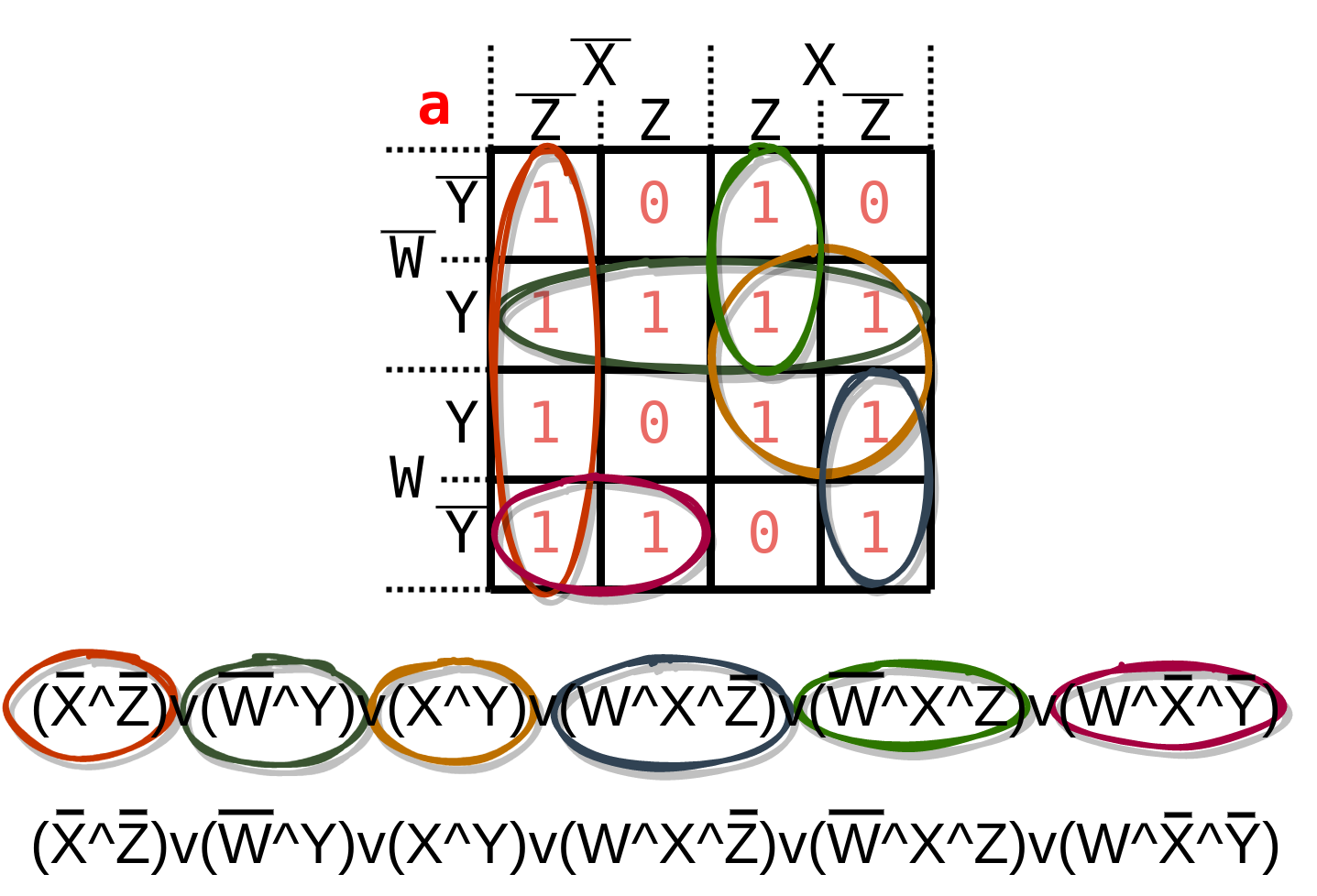
Nachdem wir nun möglichst viele Felder der KV-Tafel zusammen gefasst haben, können wir daraus nun die logischen Gleichungen erstellen. Dabei gucken wir uns die einzelnen Schleifen an. Dabei stellt sich bei jeder Schleife die Frage: Welcher Zustand ist hier ausschlaggebend.
Zum Beispiel ist in der ersten Schleife nicht die Eingange W und Y von belangen. Es zählen nur die Eingänge X und Z und sie müssen verneint sein. Dann kann man sagen, dass das Segment angeschaltet sein soll. Oder aber auch bei der zweiten Schleife: Hier zählen nicht die Eingänge X und Z, sondern nur das der Eingang W aus -und Y eingeschaltet sind. Dies lässt sich auf alle Schleifen anwenden. Die konkrete Darstellung sieht dann wie folgt aus:
Die Klammern beziehen sich auf die jeweiligen Schleifen. Das Zeichen ^ steht dabei für das logische Und (AND) und das v für das logische Oder (OR). Aus dieser Bezeichnung lässt sich so schon ablesen, dass wie schon sehr nah an der technische Umsetzung stehen. An dieser Stelle können wir jetzt sogar schon in die technische Umsetzung gehen und die Siebensegmentanzeige zum Beispiel in einem Simulationsprogramm wie Falstad simulieren. Jedoch kann man diese logische Gleichung noch umstellen, sodass man nur noch ein Bauteil brauch. Dabei kann man sich entscheiden zwischen einem Nicht-Und-Gatter (NAND) oder einem Nicht-Oder-Gatter (NOR). Im folgenden Abschnitt werde ich diese logische Gleichung nach full NAND umformulieren.
Zunächst verneinen wir daher die einzelnen Klammern der logische Gleichung.
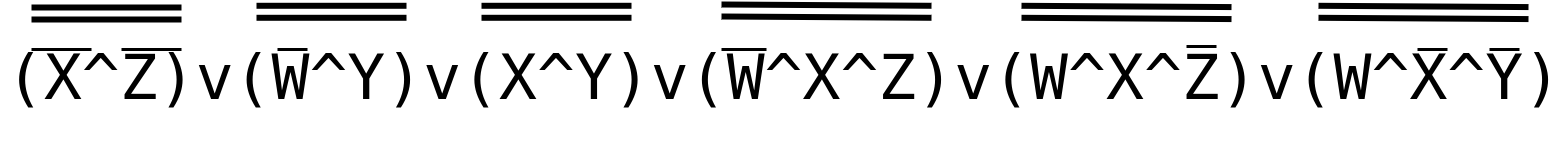
Dann können wir Schritt für Schritt die logischen Oder zu logischen Und umdrehen:
Die logische Gleichung ist nun in der letzten Gleichung komplett mit NAND Gattern beschreibbar. Die Anzahl der NAND Gatter lässt sich an der Anzahl der Verneinungen ablesen. In diesem Fall sind es 15 Stück.
Diese Systematik lässt sich nun auch auf alle anderen Segmente der Siebensegmentanzeige übertragen. Mit etwas Zeit kommt man so auf folgende Ergebnisse der einzelnen Schritte:
Im Anschluss daran habe ich mir die Mühe gemacht und diese nun gewonnenen Informationen in dem Simulationsprogramm Falstad umzusetzen. Dabei habe ich zwei Versionen gebaut. Einmal mit gemischten Gatter und einmal in full NAND. Man erkennt dadurch auch, dass beide Methoden zum selben Ergebnis führen, jedoch anders Aufgebaut sind.
Falstad: Schaltungen als Textdatei zum Download
Weitere Quellen
- Mehr zum Aussehen und der geschichtliche Hintergrund – 16.11.2021
- Mehr zum De-morgansche Gesetz – 16.11.2021
- Falstad